Actualizacion de Muro

 

Trabajando en articulo!!!!

Area y Volumen de figuras geometricas

Area y Volumen de figuras geometricas

Matematicas 14 de Marzo del 2009

Matemàticas 2º Problema

Problema de Matemàticas Nº1

Solucion de Problema de matemàticas

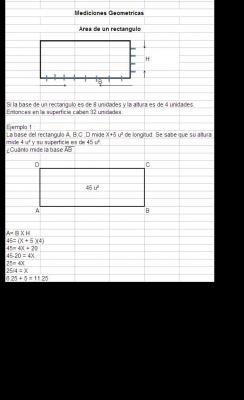
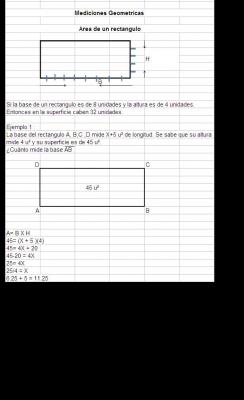
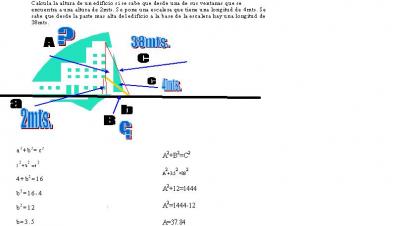
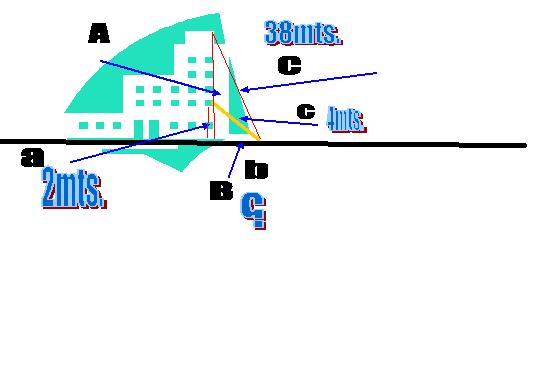
Calcula la altura de un edificio si se sabe que desde una de sus ventanas que se encuentra a una altura de 2mts. Se pone una escalera que tiene una longitud de 4mts. Se sabe que desde la parte mas alta del edificio a la base de la escalera hay una longitud de 38mts.

 

a²+b²=c²

 ₂²_+b² ₌₄²

 

4+b²=16

 

b²=16-4

 

b²=12

 

b=3.5

 ************************* 

A²+B²=C²

 

_A²_+3.5² ₌₃₈²

 

A²+12=1444

 

A²=1444-12

 

A=37.84

Desafio 05 àngulos (parejas especiales de àgulos)

CLASIFICACION DE ÀNGULOS

^{RIE DE LA VIDA NO DEJES QUE ELLA SE RIA DE TI.}

PAREJA ESPECIALES DE ÁNGULOS

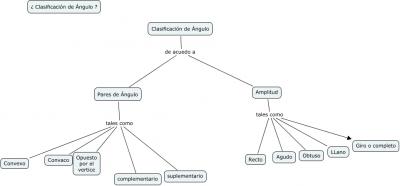
PAREJA ESPECIALES DE ÁNGULOS

 

PAREJA DE ÁNGULOS
Ángulos  adyacentes	Son ángulos que tienen un lado común y los otros dos pertenecen a la misma recta.
Ángulos  consecutivos	Son ángulos que tienen un lado común y el mismo vértice.
Ángulos opuestos por el vértice	- Dos líneas que se intersectan generan ángulos opuestos por el vértice.  - Son ángulos no adyacentes.   <1, <2, <3 y <4   - Son ángulos   congruentes:  <1 = <2 y <3 = <4
Ángulos complementarios	- Es un tipo especial de ángulo adyacente cuya particularidad es que suman 90°.     El <BAC es adyacente al <DAC y viceversa.
Ángulos suplementarios	- Es un tipo especial de ángulo adyacente cuya particularidad es que suman 180°.     El <BAC es adyacente al <DAC y viceversa.

Definicion de postulado, Axioma, Teorema.

Definición de Postulado

Diccionario de Filosofía Definición de Postulado

Proposición que no es evidente por sí misma y que no tiene una aceptación universal. Por lo tanto, un postulado se diferencia de un axioma, que es una proposición universalmente admitida. La formulación clásica del concepto de postulado se encuentra en los Elementos de Euclides, para quien un postulado es una proposición fundamental de un sistema deductivo que no es evidente por sí misma, pero que tampoco puede ser demostrada. Los postulados suelen ser las proposiciones iniciales de una ciencia determinada, mientras que los axiomas son las proposiciones iniciales de un sistema deductivo, a partir de las cuales pueden derivarse otras proposiciones. Actualmente hay una creciente tendencia a emplear indistintamente axioma y postulado.

Axiomas [editar]

En geometría sintética, los axiomas son proposiciones o afirmaciones que relacionan conceptos, definidos en función al punto, la recta y el plano. Se distinguen cuatro grupos de axiomas. Un quinto grupo de axiomas (el axioma de paralelismo) es el que distinguirá una geometría de otra.

En geometría analítica, los axiomas se definen en función al punto; no tiene sentido hablar de recta o plano. f(x) puede definir cualquier función llámese recta, circunferencia, cuadrado de la circunferencia, planos, entre otros.

Un axioma, en epistemología, es una "verdad evidente" que no requiere demostración, pues se justifica a sí misma, y sobre la cual se construye el resto de conocimientos por medio de la deducción; aunque, no todos los epistemólogos están de acuerdo con esta definición "clásica". El axioma gira siempre sobre sí mismo, mientras los postulados y conclusiones posteriores se deducen de este.

En matemática, un axioma no es necesariamente una verdad evidente, sino una expresión lógica utilizada en una deducción para llegar a una conclusión.

Teorema.

(Del lat. theorēma, y este del gr. θεώρημα).

1. m. Proposición demostrable lógicamente partiendo de axiomas o de otros teoremas ya demostrados, mediante reglas de inferencia aceptadas.

Teorema s. m. Afirmación que se hace dentro de un sistema lógico y que puede ser demostrada a patrir de los axiomas: el teorema de la altura afirma que, en un triángulo rectángulo, el cuadrado de la altura sobre la hipotenusa es igual al producto de los segmentos que esta determina sobre la hipotenusa

• Teorema: una proposición que es demostrable o refutable aplicando la lógica formal a partir de axiomas o postulados se denomina teorema. Un teorema también se puede demostrar apoyándose en teoremas previos. En todo teorema se distinguen tres partes:
  Hipótesis: supuestos o datos conocidos
  Tésis: lo que se quiere demostrar
  Demostración: procedimiento lógico en el que se utilizan los conocimientos previos para mostrar la verdad de un teorema.
  
  Corolario: es un teorema que surge como consecuencia de otro.
  
  Teorema recíproco: Todo teorema tiene su recíproco. La hipótesis y la tésis del recíproco son, respectivamente, la tésis y la hipótesis del otro teorema (teorema directo). No siempre los teoremas recíprocos son verdaderos.

Fuente(s):

Google:”Teorema recíproco”

Primeros conceptos
usuarios.lycos.es/calculo

•  
  • hace 1 año

 

Desafio creado el 07 de Febrero del 2009

Serafin

Aaron

Jordan

Juan Carlos

Dulce